正方形を正確に三つ折りする
2006.02.09 Thursday 00:09
電車の中で本を読んでいるとき,ポケットに入っていた正方形のメモ用紙を三つ折りにしてしおり代わりに使おうとしたの.大抵三つ折りというのは目算でえいやっと折って作ることが多い.しかし今回はどうもそれでは納得できず,正確な三つ折り方法があるのではないかと考えてみた.
問い:正方形を正確に三つ折りにすること.ここで三つ折りとは長辺として元の正方形の一辺を利用し,短辺として元の正方形の一辺を1/3に折り曲げた長方形を作ることとする.
問い:正方形を正確に三つ折りにすること.ここで三つ折りとは長辺として元の正方形の一辺を利用し,短辺として元の正方形の一辺を1/3に折り曲げた長方形を作ることとする.
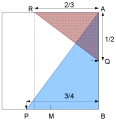
[手順]
まず一辺を折り曲げて二等分する(図中M).さらにそれを折り曲げて二等分する(図中P).
頂点Bから3/4の長さの点Pと対角側にある正方形の頂点Aを通るように折り目(直線AP)を付ける.
次に横の辺ABを二等分し,中点Qを取る.Qを通り上でつけた線APに垂直に折る.(点Aが直線APの上に乗り,折り目が点Qを通るように折る)
出来た線と正方形の上辺との交点をRとするとARは一辺の長さの2/3となっている.ARの中点を取ることで上辺を3等分することができ,できた3等分点を通って上辺に垂直に折れば1/3ずつに折ることが出来る.
実際にやってみると2点を通る線APを正確に折るのが難しく,結構な誤差が出てしまう.点と点を合わせるのは容易だが折り目を特定の位置に合わせるのは技がいる.上の手順は定規とコンパスによる作図でもできるが,作図の方が誤差は少ないだろう.
[上の手順の説明]
正方形の四隅が直角であること,直線BPと直線QRが垂直であることから△APBと△RQBは相似となる.故にBP:AB=AQ:AR,
AR=xとすると,3/4:1 = 1/2:x
x = 1/2 / (3/4) = 2/3
この方法を応用して二辺の長さが異なる長方形の長辺を三等分する方法も考えたので早速1000円札で試そうとしたところ,1000円札の長辺と短辺が2:1の比となっていることに気が付いた.
Comments